La première chose à savoir pour comprendre ce qu’est le déciBel, c’est que tout peut potentiellement être quantifié sous forme de déciBel (un poids, une force, une température…). En pratique, cette unité est surtout utilisée en électronique, en traitement du signal ou en acoustique.
En acoustique, on parle très souvent de dB SPL (Sound Pressure Level), souvent abrégé dB, une unité qui permet de quantifier le niveau sonore. En électronique, on utilise le dBu ou le dBV pour la tension électrique ou le dBm pour la puissance. En traitement du signal, le dB FS...
Comment expliquer qu’une seule unité puisse quantifier tant de choses différentes ? En fait, le déciBel n’est pas une unité classique, puisqu’il s’agît d’une grandeur sans dimension, c'est-à-dire le ratio entre la grandeur que l’on veut quantifier, et une valeur de référence, de même unité. Le dB a en plus la particularité d’être obtenu en utilisant une fonction logarithmique.
Exemple : on obtient le niveau de pression acoustique (dB SPL) en divisant la pression mesurée par une pression de référence, puis en multipliant par 20 le logarithme décimal du résultat : dB SPL = 20 log10(Pmesurée/Pref)
Comment est établie la grandeur de référence ? Eh bien, ça dépend des cas. Pour la pression acoustique, on choisit la pression la plus faible que l’oreille humaine peut percevoir (2 microPascals). Pour les dBu, la référence est de 0,775 V, pour des raisons historiques liées aux télécommunications. Pour les dBV, c’est 1 V, et 1 mW pour le dBm. Etc.
Si les termes dBu, dBV, SPL etc. sont les plus couramment utilisés, il est plus rigoureux d’écrire dB re 20E-6 Pa pour le dB SPL ou dB re 0,775 V pour le dBu, afin d’éviter les malentendus sur la valeur et l’unité de référence.
DB de puissance et dB de champs
On peut différencier deux grands types de déciBels, ceux de puissance (électrique avec le dBm, acoustique avec le dB Lw…) et ceux de champs ou d’amplitude (dBu en Volts, dB SPL en pascals etc.). Les déciBels sont formellement, à l’origine, un rapport entre deux puissances, mais on utilise plus souvent les déciBels de champs (amplitudes et puissances étant physiquement liées). Les dB de champs sont en fait des dB de puissance déguisés, puisque la puissance est proportionnelle au carré de l’amplitude.
Les dB qui impliquent de la puissance sont égaux à 10'log10(x), les dB de champs sont égaux à 20'log10(x). Doubler la puissance revient à une augmentation de 3 dB, alors que doubler la tension correspond à 6 dB.
Le dB FS (Full Scale, pleine échelle), lui, est un peu différent puisque le niveau 0 correspond au maximum de ce que le convertisseur analogique/numérique ou numérique/analogique peut supporter ; le niveau de référence n’est donc pas normalisé. Les dB FS sont donc toujours négatifs contrairement aux autres types de dB qui peuvent être négatifs, mais sont le plus souvent positifs vu les ordres de grandeur des systèmes audio. De plus, le dB FS n’est pas intrinsèquement lié à une puissance, et le numérateur n’est pas une valeur efficace mais une valeur crête.
Pourquoi utiliser le dB ?
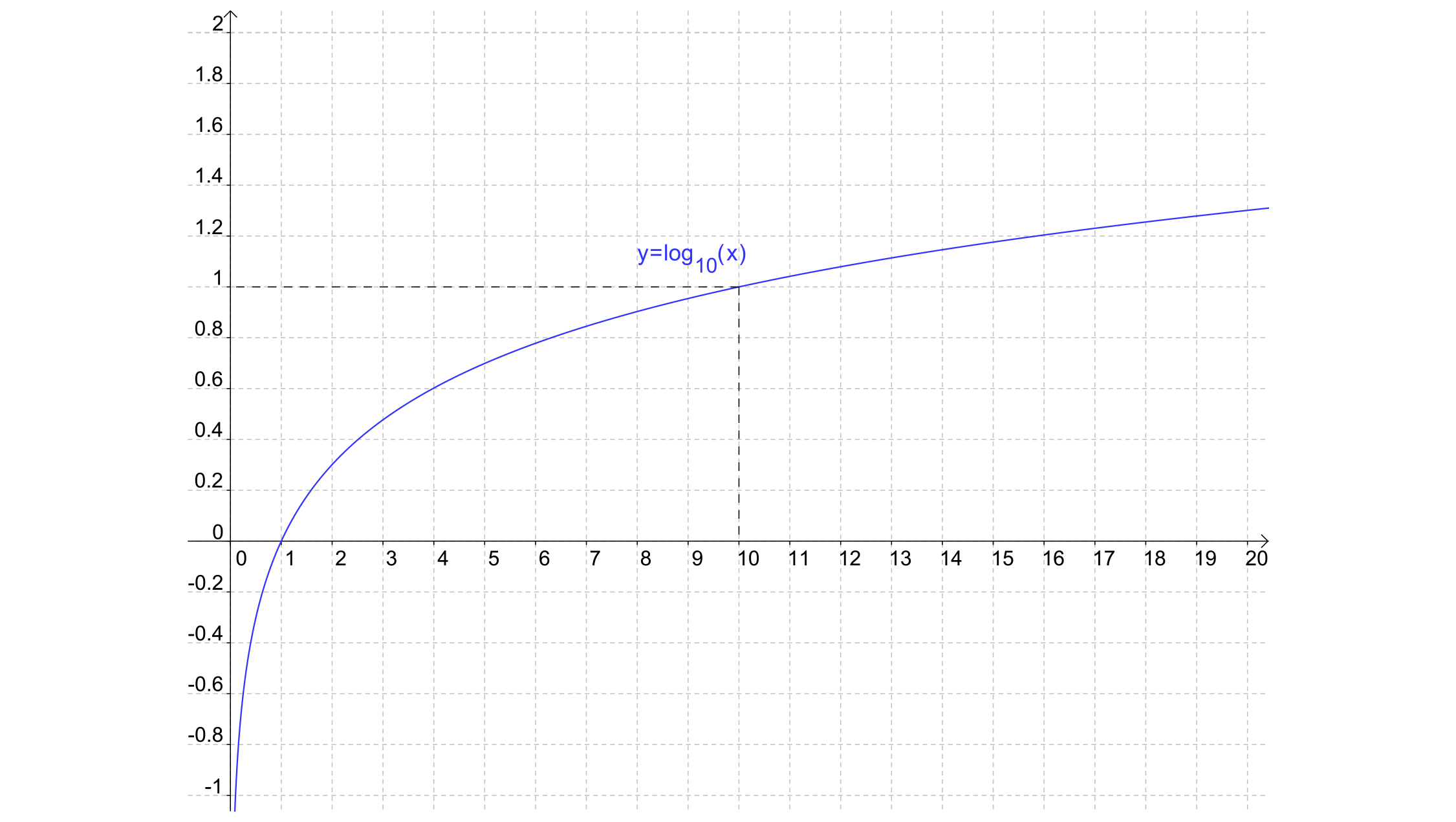
L’avantage de l’échelle logarithmique, c’est qu’elle aplatît les valeurs et rend leur lecture plus simple. En effet, 0 dB SPL correspond à une pression de de 0,00002 Pa, et 190dB à 63000 Pa, un rapport énorme, difficile à se représenter. En passant à une échelle log, tout devient plus lisible (et les calculs sont simplifiés, souvent faisables de tête : une multiplication devient une addition, une division une soustraction).
Gain et amplification :
Le dB peut également servir à décrire le gain (c’est à dire la variation de niveau) entre deux situations : dans ce cas, la référence Uref devient la situation 1 et le numérateur la situation 2. On ne parle plus de dBU ou SPL, mais de dB tout court.
Par exemple : un amplificateur a un gain de 6 dB (c’est à dire que la tension à sa sortie a un niveau supérieur de 6 dB à la tension à son entrée), le calcul est le suivant : 6 dB = 20°log10 (Vsortie/Ventrée). Si on connaît l’entrée on peut trouver la sortie : Vsortie = 10(6/20)°Ventrée. Si Ventrée = 1, Vsortie = 2. On en déduit qu’un gain de 6 dB correspond à doubler la tension (on parle de gain lorsque l’on utilise des dB, et d’amplification lorsque l’on est en linéaire).
Si on refait le calcul avec de la puissance, on obtient 3 dB = 10*log10 (2/1). Doubler la puissance correspond à un gain de 3 dB. Un gain de 6 dB en puissance revient à multiplier par 4.
Un système audio étant linéaire en première approche, pour augmenter de 6 dB le niveau SPL (ce qui est peu, il est souvent considéré qu’une augmentation de 10 dB correspond à une sensation de doublement de niveau sonore) il faut multiplier par 4 la puissance électrique en entrée.
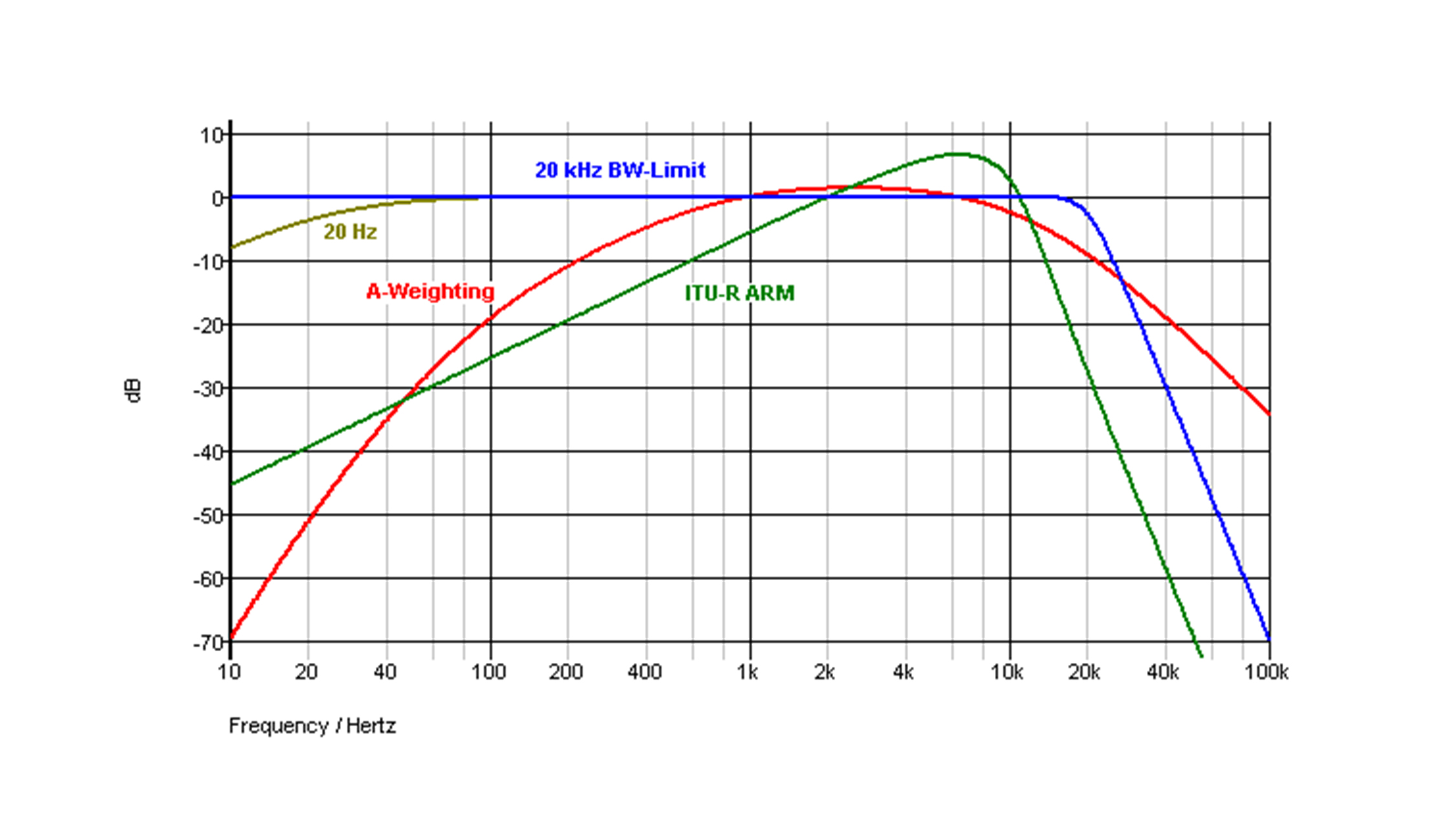
pondération En acoustique, on entend souvent parler de dBA, dBC… la lettre fait référence à une pondération appliquée à des dB SPL pour prendre en compte la sensibilité de l’oreille humaine : les basses fréquences sont atténuées par rapport aux hautes fréquences. La sensibilité de l’oreille varie selon le niveau sonore, d’où l’existence de plusieurs pondérations. Pour éviter toute confusion, on précise souvent dBZ lorsqu’aucune pondération n’est appliquée.
Importance du rendement et de la sensibilité
Ce qui nous amène à l’importance de la sensibilité et du rendement d’une enceinte. La sensibilité représente le niveau SPL produit par une enceinte pour une tension donnée à une distance d’un mètre. Le rendement est similaire à la sensibilité, sauf qu’il considère une puissance en entrée et non pas une tension ; une enceinte à forte sensibilité n’est pas nécessairement une enceinte à haut rendement.
Pour comprendre la différence entre rendement et sensibilité >>
Une enceinte de sensibilité 90 dB SPL pour 2,83 V (c’est à dire 1 W sur une charge de 8 Ohms) nécessitera 90 V pour produire 120 dB SPL. Si l’on regarde le rendement et donc la puissance, ce qui est bien plus intéressant que la sensibilité, et que l’enceinte a effectivement une impédance de 8 Ohms (cas théorique), il faut 1000 Watt.
Si l’on refait le calcul pour une enceinte de rendement et de sensibilité plus élevés, disons 98 dB, on obtient 35 V et 160 Watt, on économise donc 85 % d’énergie.
Les 120 dB SPL sont une valeur moyenne, mais la musique contient de nombreuses crêtes (attaques des instruments, percussions…). Et celles-ci montent facilement à 126 dB (musique enregistrée très compressée) ou 132 et plus pour du concert.
Pour obtenir 126 dB, il faut encore multiplier la puissance par 4 (8 pour 132 dB) ! Il est donc important de garder en tête les grandeurs physiques en jeu derrière les dB, les puissances sont vite très élevées sur des systèmes son classiques.
Conclusion
L’existence de plusieurs types de déciBels est souvent source de confusion. Il suffit de comprendre que le dB est avant tout une façon de se représenter des grandeurs physiques, de manière simplifiée et pratique. Il est important de différencier les deux grands types de dB, ceux de puissance et ceux de champs ou d’amplitude, afin d’obtenir des résultats corrects lors des calculs.